안녕하세요,
이번 포스팅에선 오랜만에 DoE 소프트웨어인 MODDE를 주제로 들고 왔습니다. 많은 분들이 궁금해 하셨던 Lack-of-fit, 즉 적합성 결여에 대해 안내를 드리고자 합니다. 아마 회귀 직선에 대해서는 많이 들어보셨겠지만, 이외에도 디자인이 잘 설계됐는지 파악하는 척도로 사용되는 적합성 결여는 그 의미 및 사용 방법에 대해 어려운 부분이 많으신 것으로 보입니다.
기존에는 MODDE에서 디자인을 평가할 때 사용하는 4가지 척도인 R2, Q2, 모델 유효성, 재현성을 봤었습니다. 각각 모델을 얼마나 설명할 수 있는지, 랜덤한 입력값에 얼마나 대응할 수 있는지(예측력), 모델은 유효한지, 중심값에 대한 재현은 잘 되는지에 대한 얘기죠~ 그 중에서도 모델의 유효성 (노란색 바) 에 대해서는 사실 자세히 알 수 있는 방법이 없었습니다. 그도 그런게 대부분의 통계 소프트웨어에서는 p-value를 통해 해당 Response의 유의성을 검정하기 때문에 MODDE에서는 어떤식으로 유효성을 검증하는지 저도 처음 소프트웨어를 접했을 때 궁금했던 부분이었습니다.
 |
| Summary of Fit (좌측부터 설명력, 예측력, 유효성, 재현성) |
 |
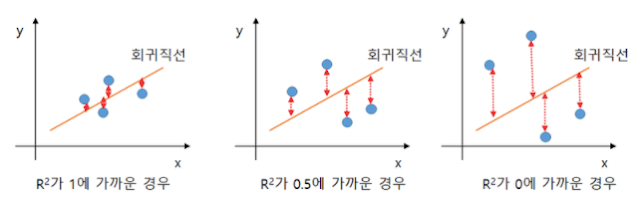| 출처 : https://blog.naver.com/statsol/221333530305 |
회귀 직선은 무엇일까요? 쉽게 예를 들어보면 시험 성적에 끼치는 여러 요인들로 과목별 점수, 교우들과의 관계, 그날 아침 먹은 음식, 집 문을 나설 때의 날씨 등 여러 독립 변수들에 대해 시험 성적과의 인과관계를 분석한 모형을 도식화 한 것으로 볼 수 있겠죠. 물론 실제로 시험 성적에 가장 크게 영향을 주는 것은 과목별 점수일 것이고 나머지 항목들은 낮거나 거의 없는 결과가 나올 것이라 생각할 수 있습니다. 그 때 우리는 R2가 높을수록 (원인이 결과를 설명할 수 있는지) 회귀 직선에 밀접한 것을 볼 수 있고, 관계가 없을 수록 떨어지는 것을 볼 수 있습니다.
그러면 한 단계 더 나아가서.. 이번엔 옆 학교의 성적에 대한 인과관계를 종합하여 보는 것을 가정하고 얘기해보겠습니다. 만약 옆 학교의 학생들도 마찬가지로 과목별 점수가 시험에 영향을 준다면 저희가 만든 모형이 큰 문제가 없겠죠? 하지만 만약에 이 학교 학생들은 그날의 날씨에 따라 성적에 영향을 받는다고 칩시다. 이 때 발생하는 오차를 적합성 결여라고 표현합니다. 물론 회귀와 비슷한 의미를 가지지만, 적합성 결여는 동일한 독립변수가 여러 종속변수 y와 관계가 있을 때 유용한 지표로 활용할 수 있습니다.
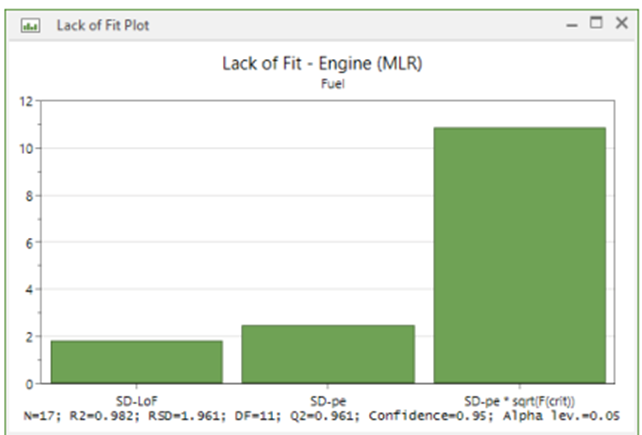
MODDE에서는 적합성 결여를 도표로 시각화하여 보여줍니다. 우선은 ANOVA 결과치를 통해 수치적인 데이터를 우선적으로 보여주면서 적합성 결여 전용 기능을 통해서도 세부적으로 확인할 수 있습니다.
 |
| 예) Lack of Fit = 3.34, F-test 0.54, p-value 0.785 |
이 그래프에서는 제일 마지막의 SD-pe * sqrt (F-crit) 값이 SD-LoF보다 낮을 시에 해당 변수의 적합성 결여가 유의함을 의미하게 됩니다. 즉 모델에 적합성 결여가 존재함을 의미하게 되며, 동시에 여러 파라미터로 디자인을 검증할 때 같이 해석하면 좋은 지표로 활용이 될 수 있을 것이라 생각합니다.
이번 시간에는 짧지만 적합성 결여를 알아보는 방법에 대해 알아봤습니다.
궁금하신 사항은 언제든지 댓글 남겨 주시면 답변 드릴 수 있도록 하겠습니다.
댓글
댓글 쓰기